
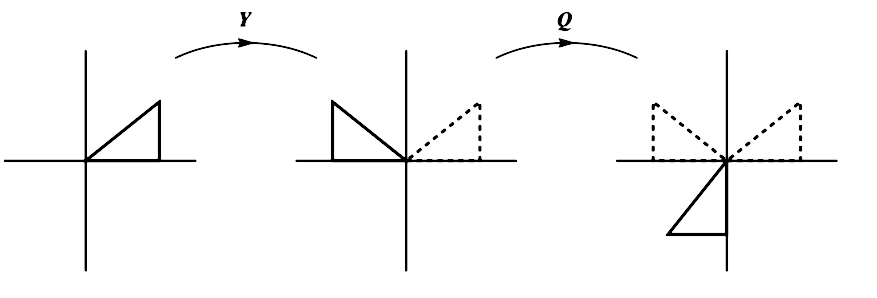
Linear Transformation Combination Of Ccw 90 Rotation And Reflection On Y X With Product Of Matrix Youtube
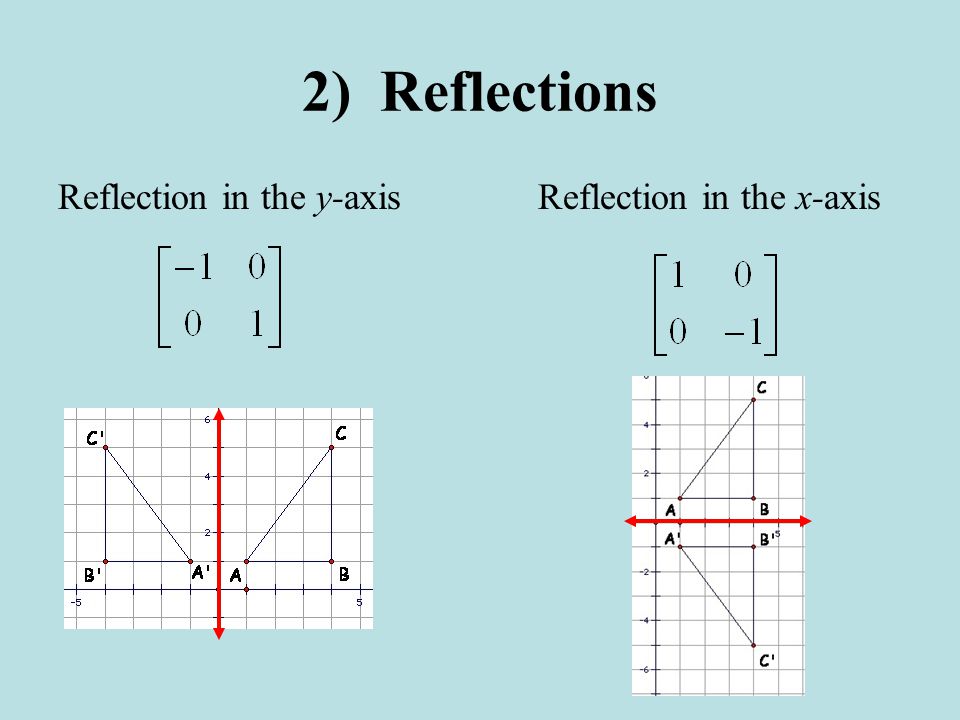
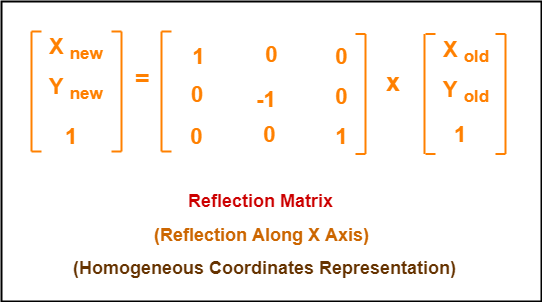
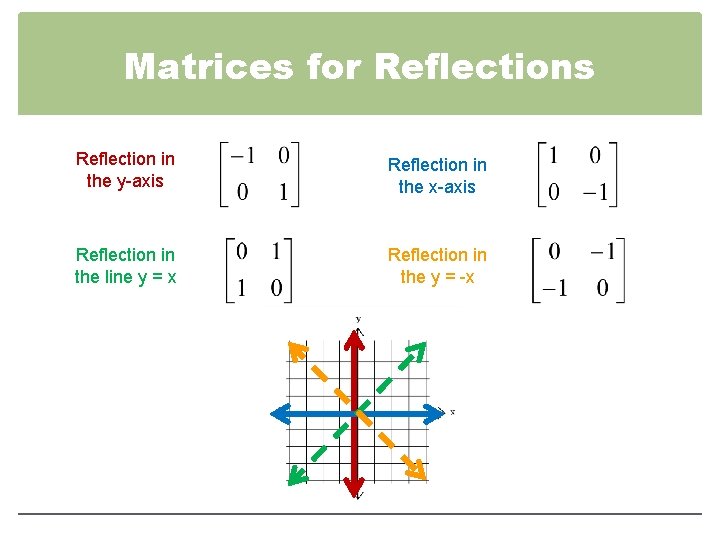
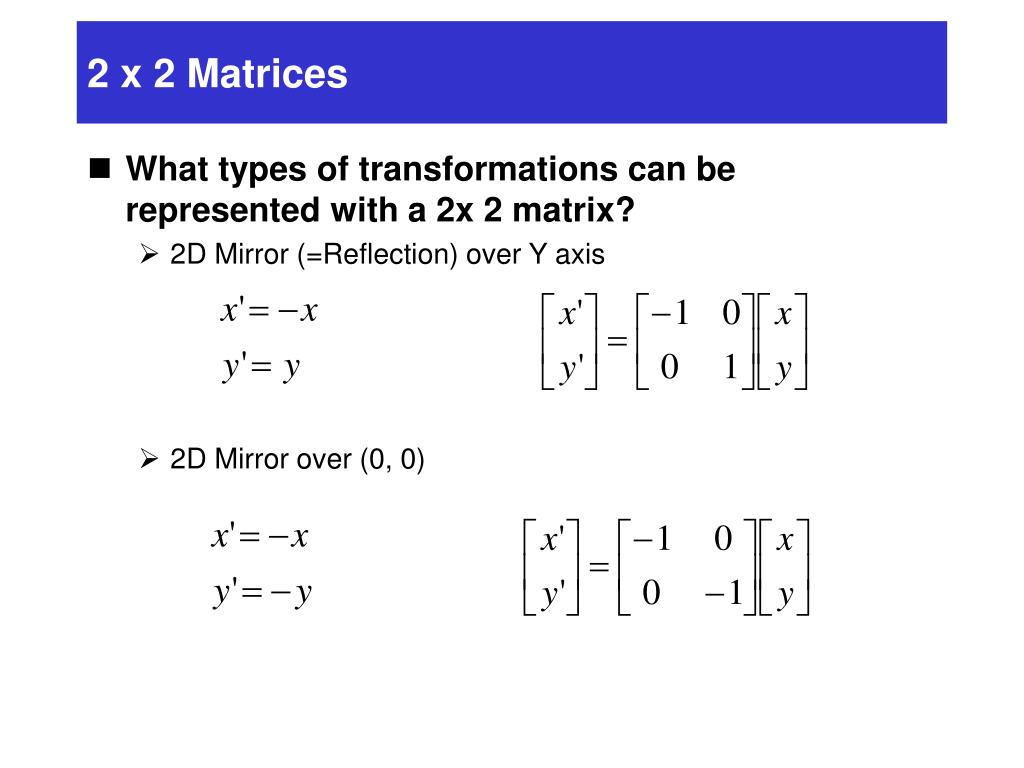
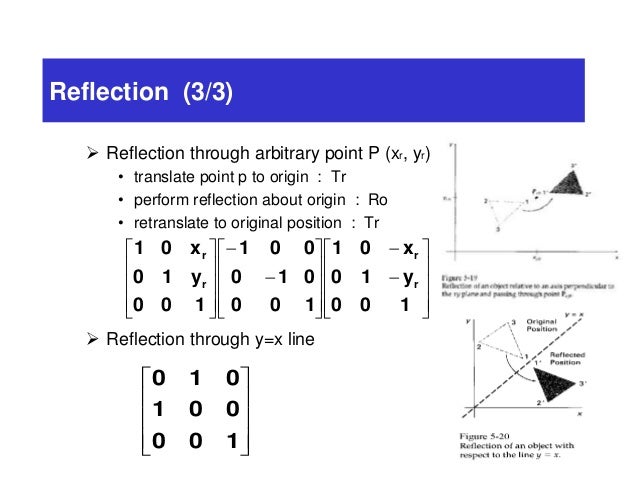
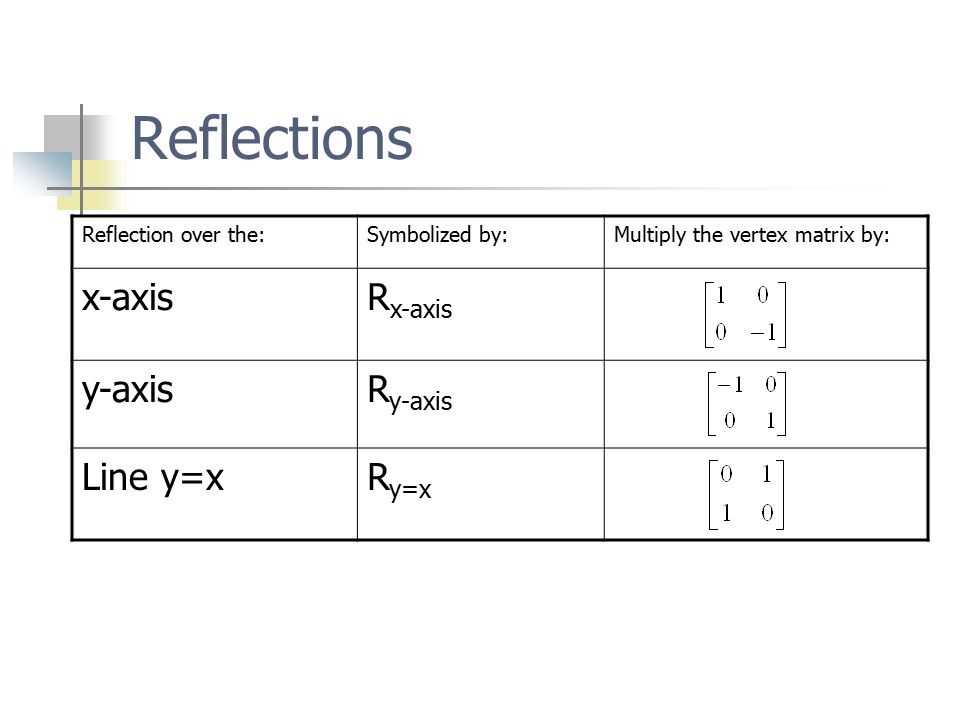
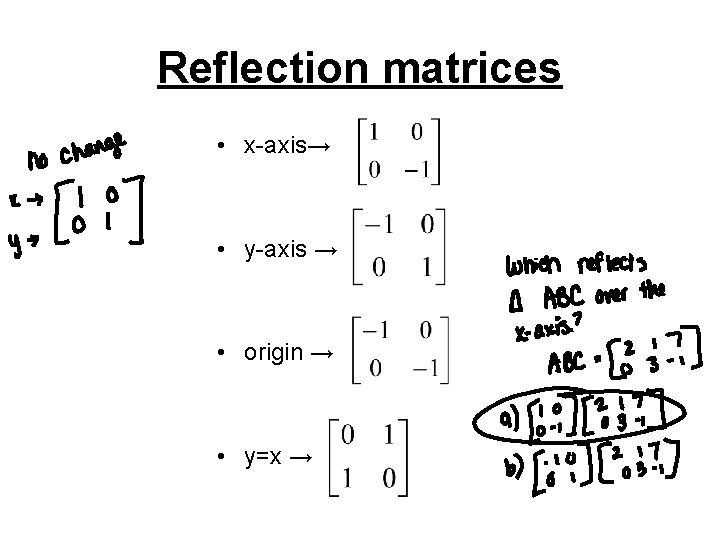
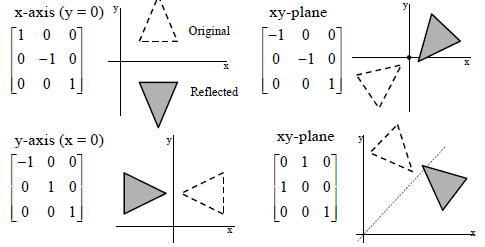
Also, how would you do things like reflection in the line y = x on a 3x3 matrix, if it is even possible thanks We can represent the Reflection along yaxis by following equationY=X, then the points are (Y, X) Y= –X, then the points are (–Y, –X) We can also represent Reflection in the form of matrix– Homogeneous Coordinate Representation We can also represent the Reflection along with xaxis in the form of 3 x 3 matrix
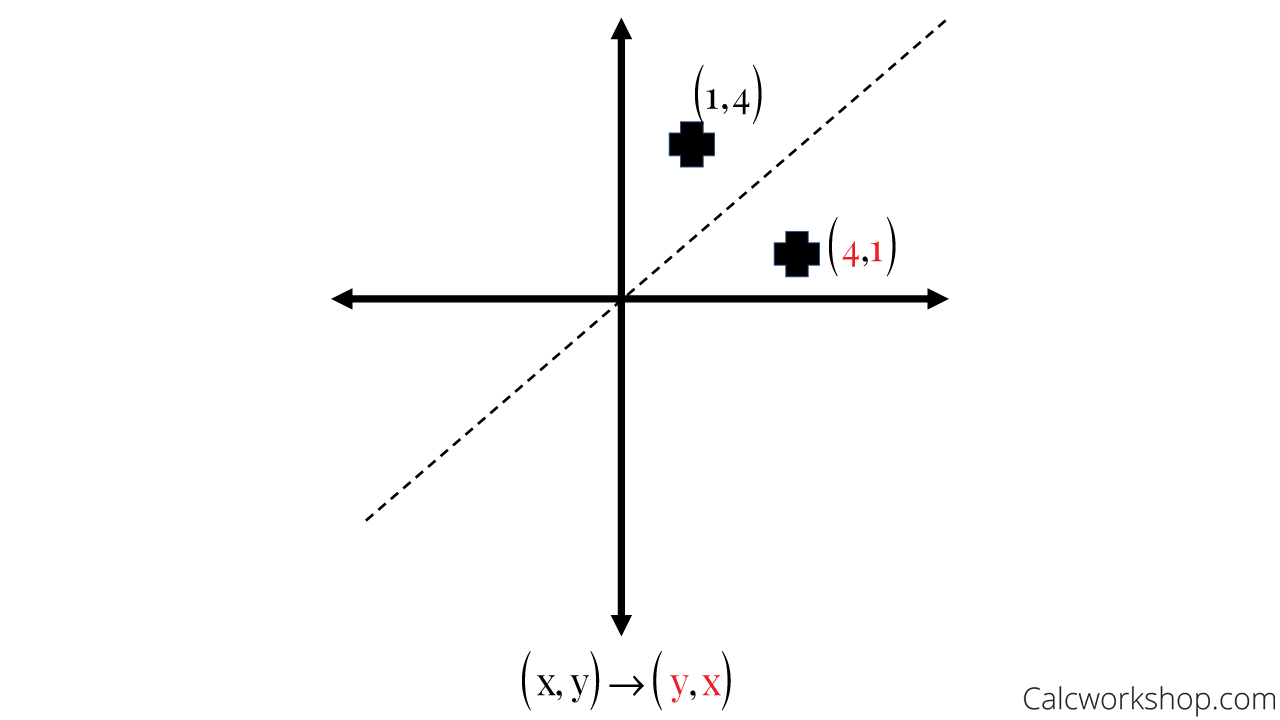
What does y=x mean in reflections
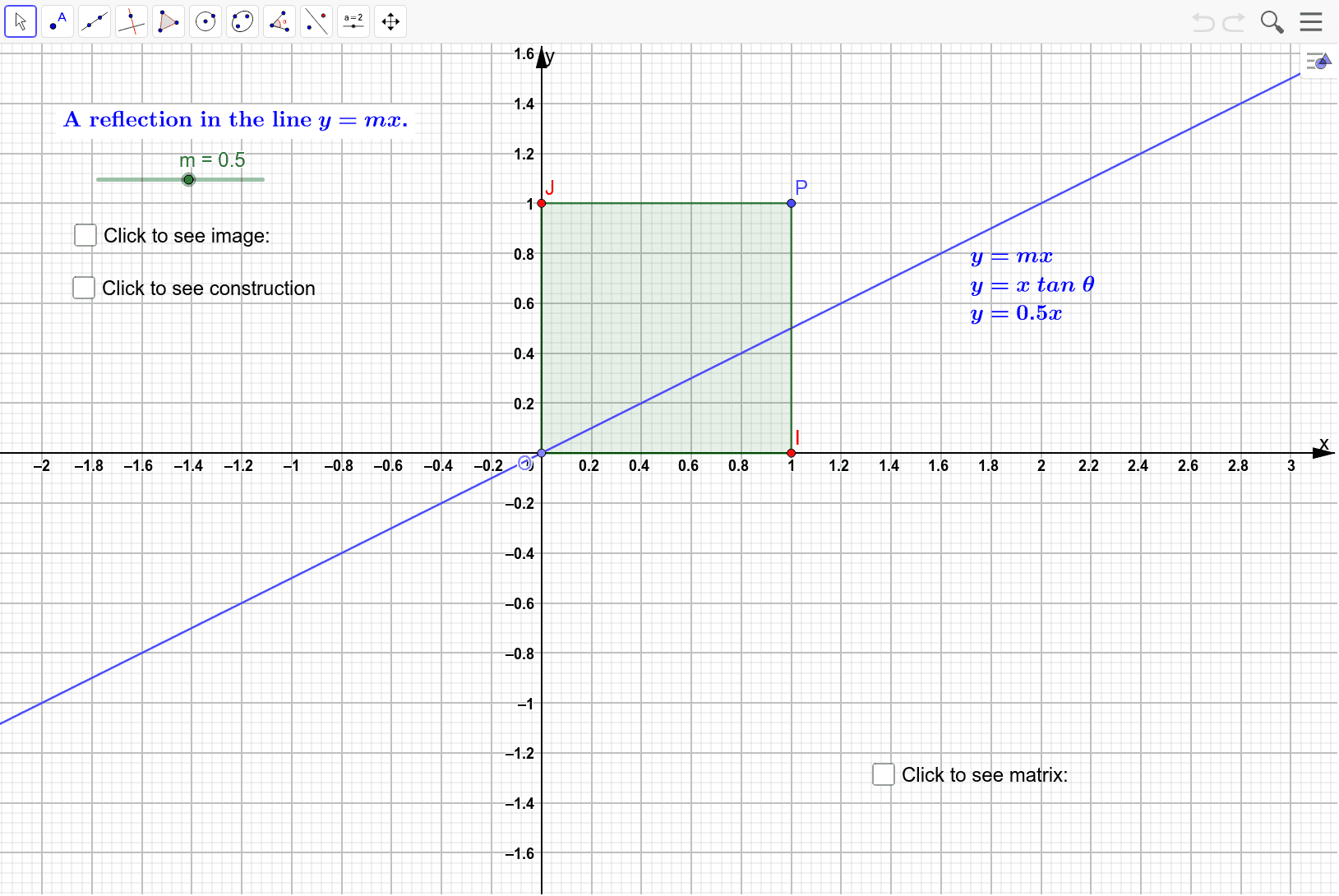
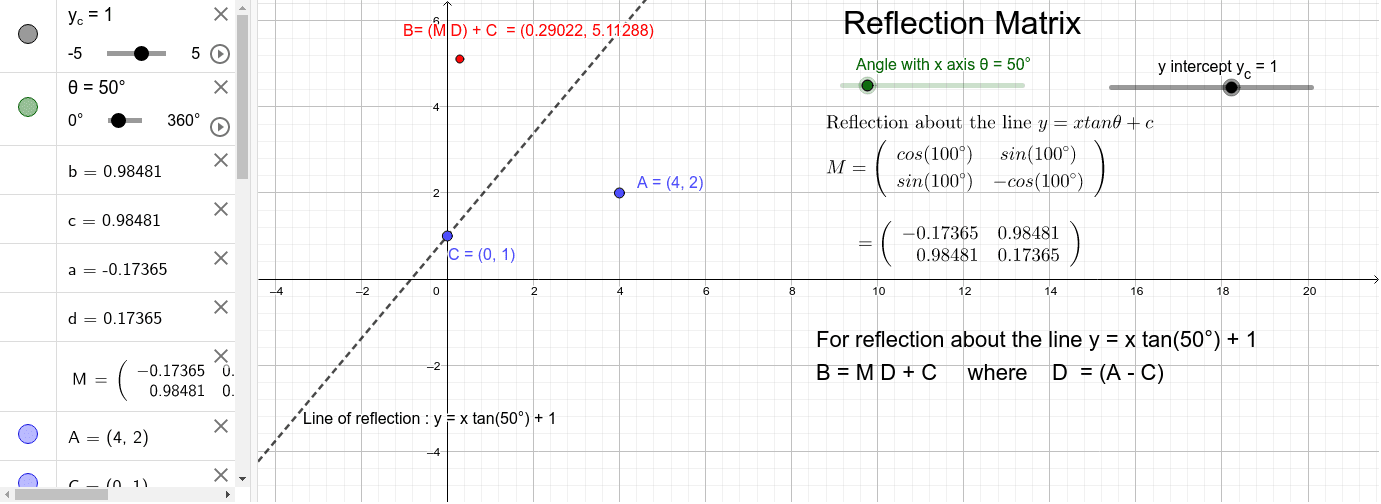
What does y=x mean in reflections-The matrix for a reflection is orthogonal with determinant −1 and eigenvalues −1, 1, 1, , 1 The product of two such matrices is a special orthogonal matrix that represents a rotation Every rotation is the result of reflecting in an even number of reflections in hyperplanes through the origin, and every improper rotation is the result of reflecting in an odd numberAnswer Homogeneous transformation matrix for reflection about the line y=mxc can be done in 5 steps 1Line intersects the y axis in the point(0,c) 2make a translation that maps (0,c) to the origin 3slope of line m=tanθRotate the given line about origin through an angle θ 4Apply a

Matrix Reflections Youtube
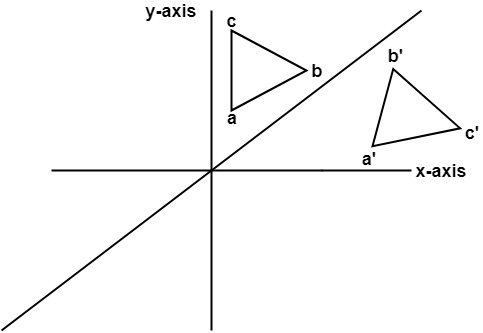
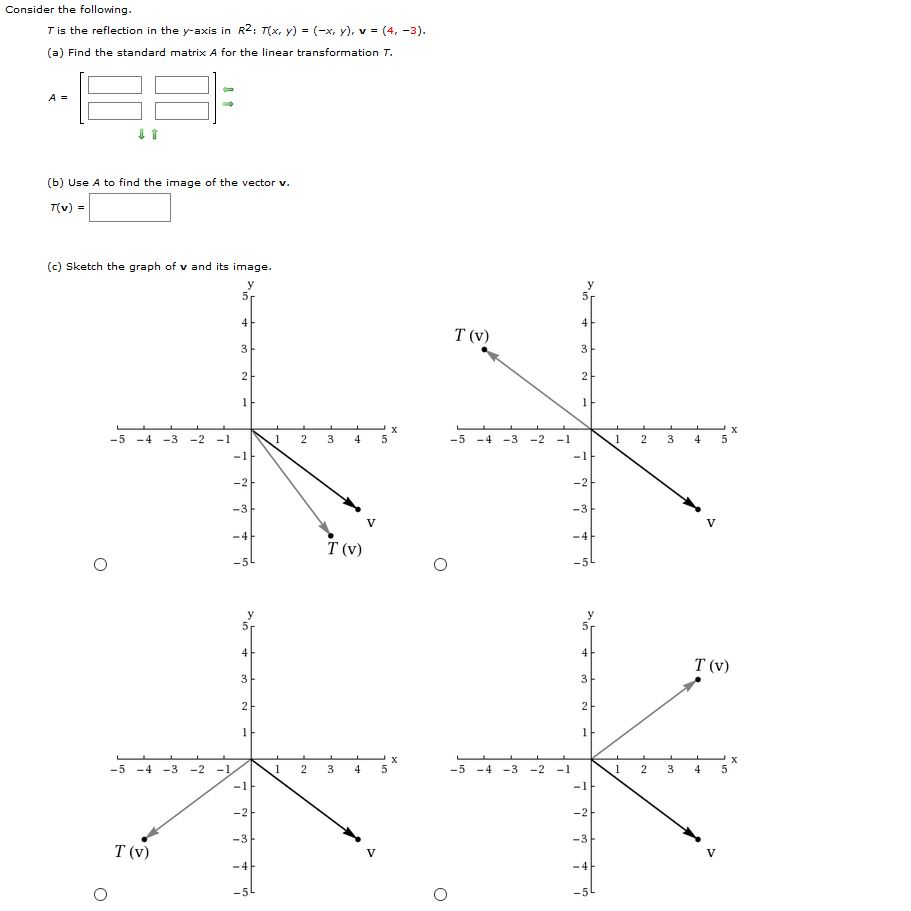
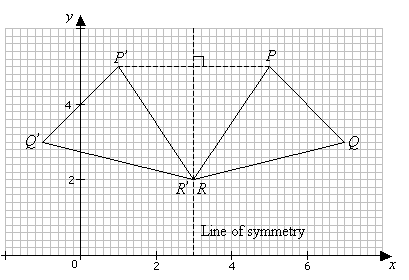
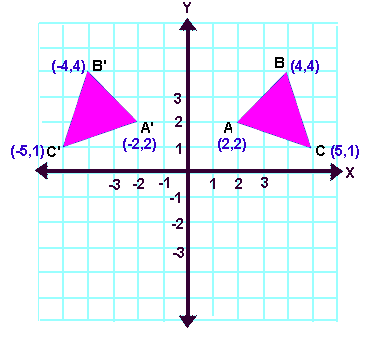
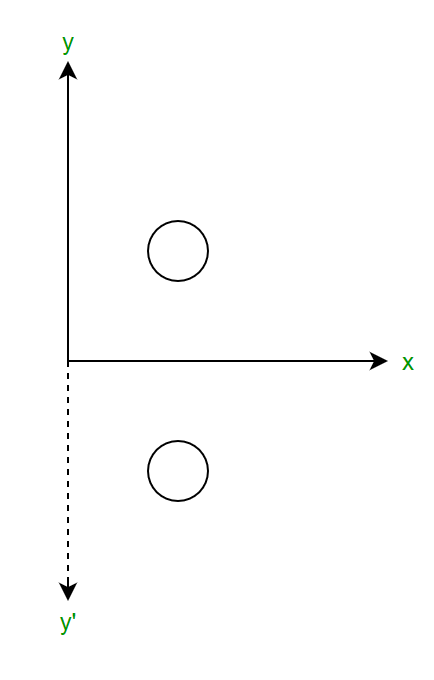
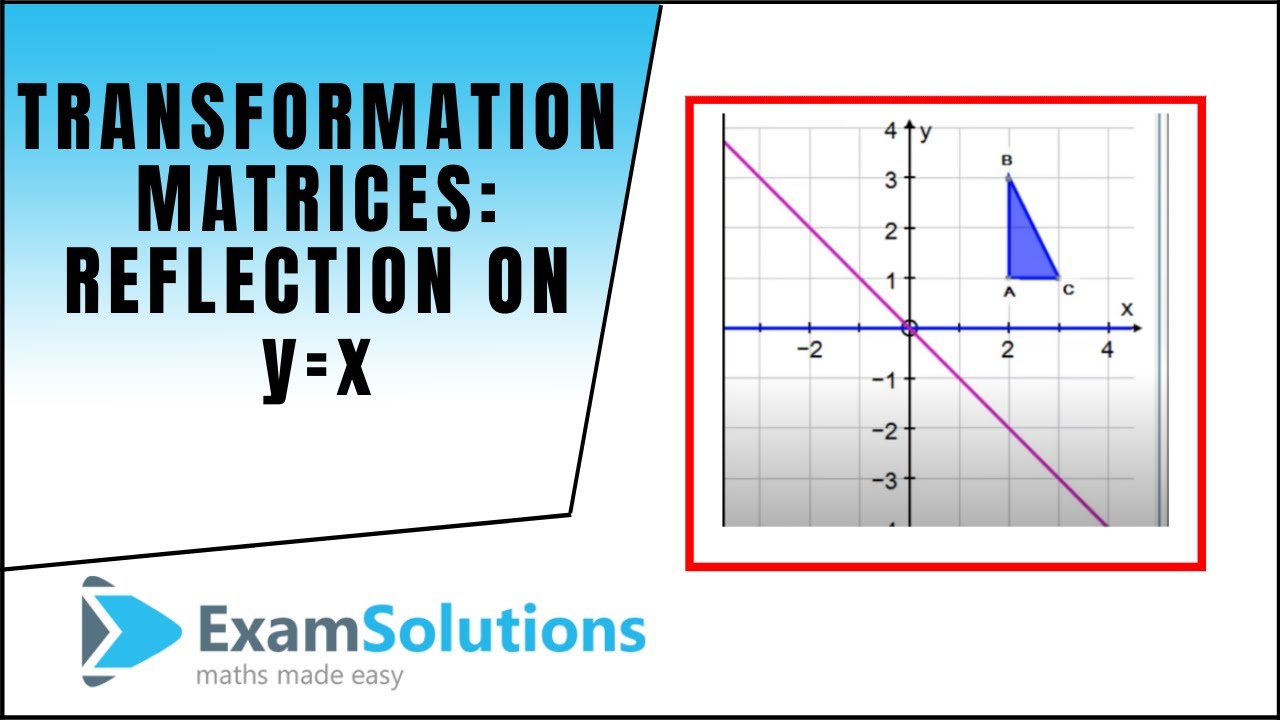
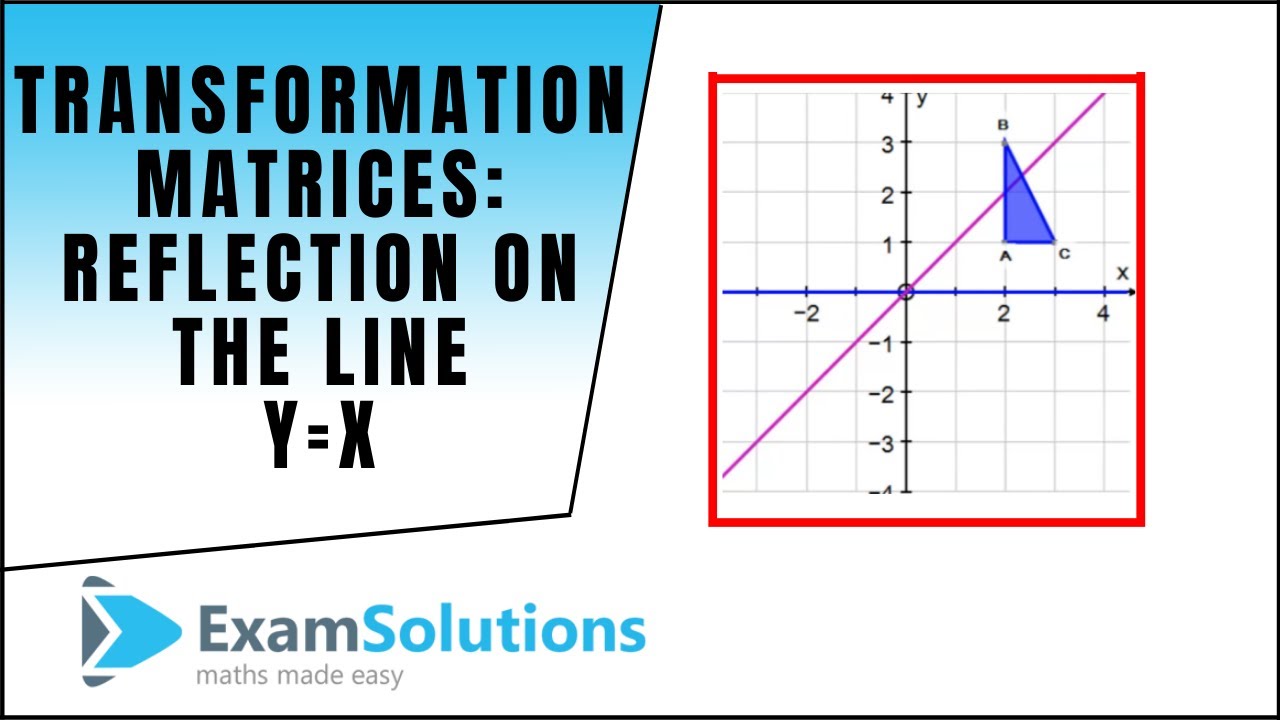
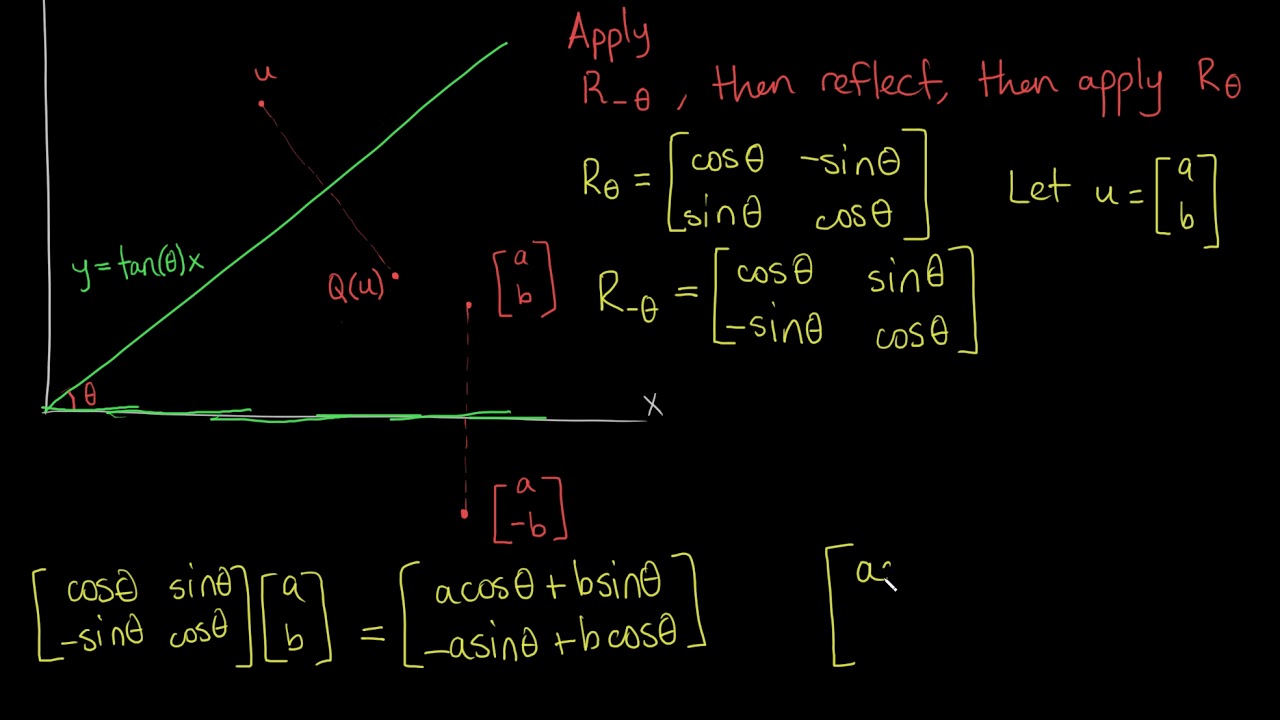
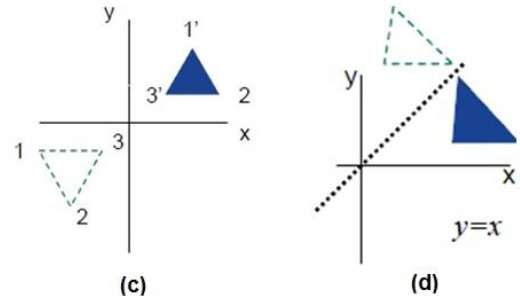
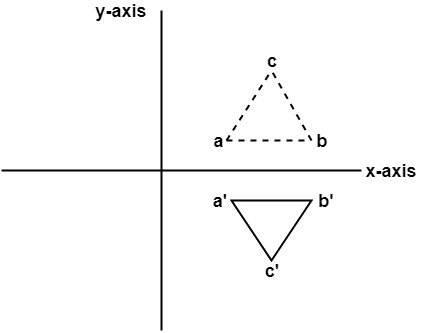
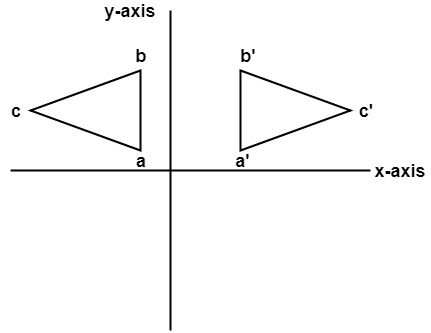
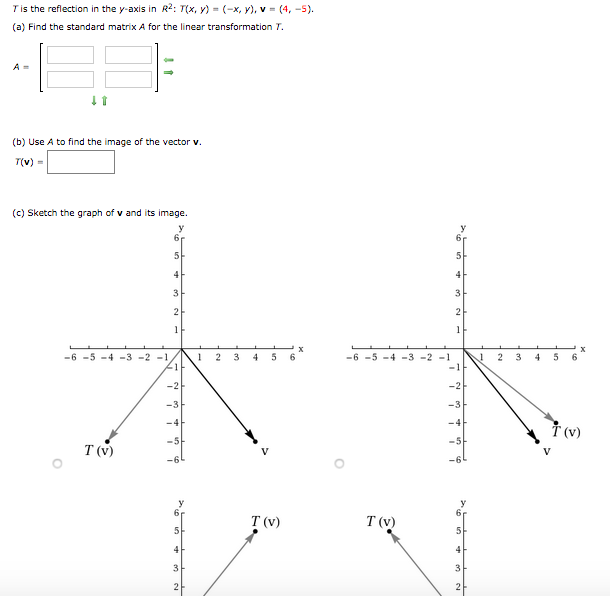
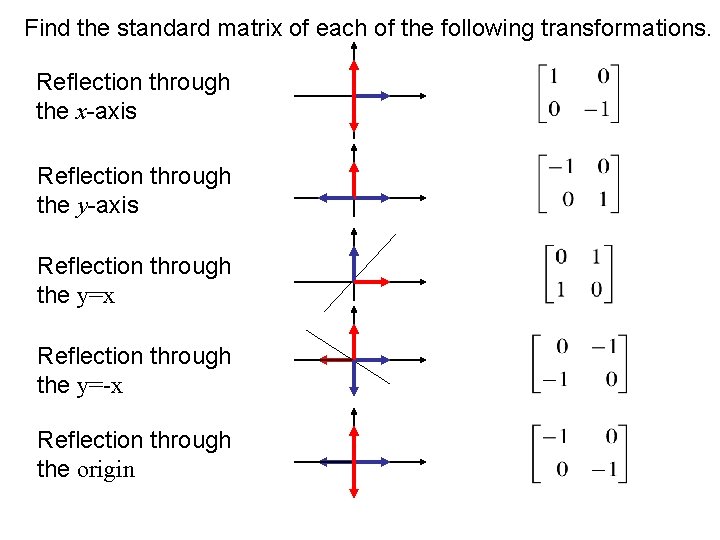
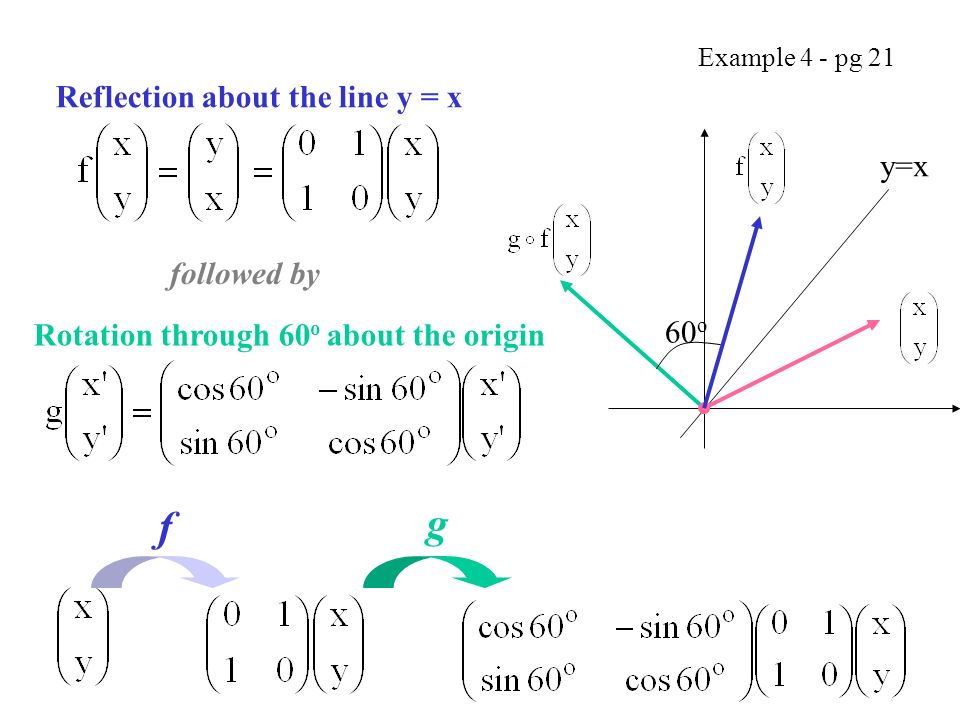
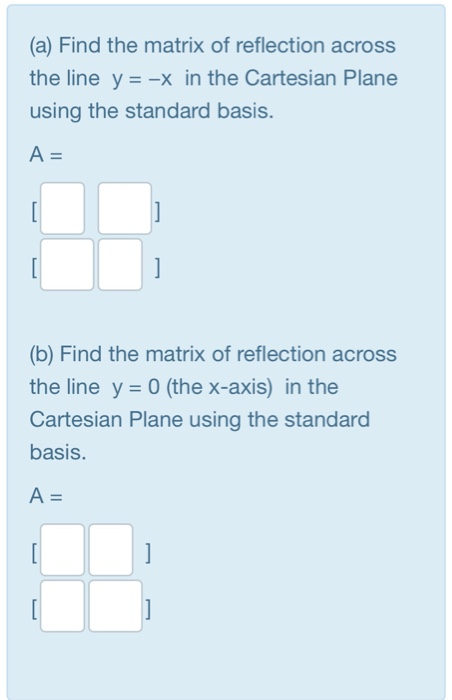
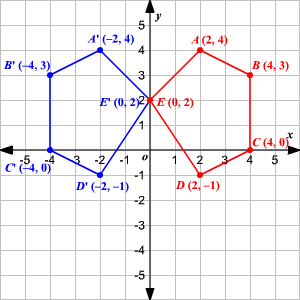
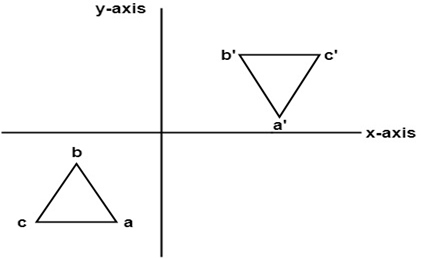
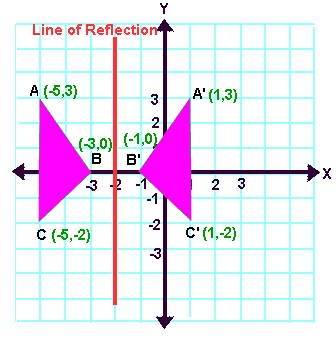
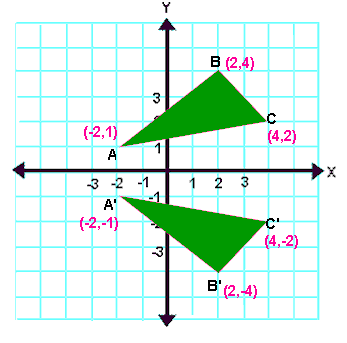
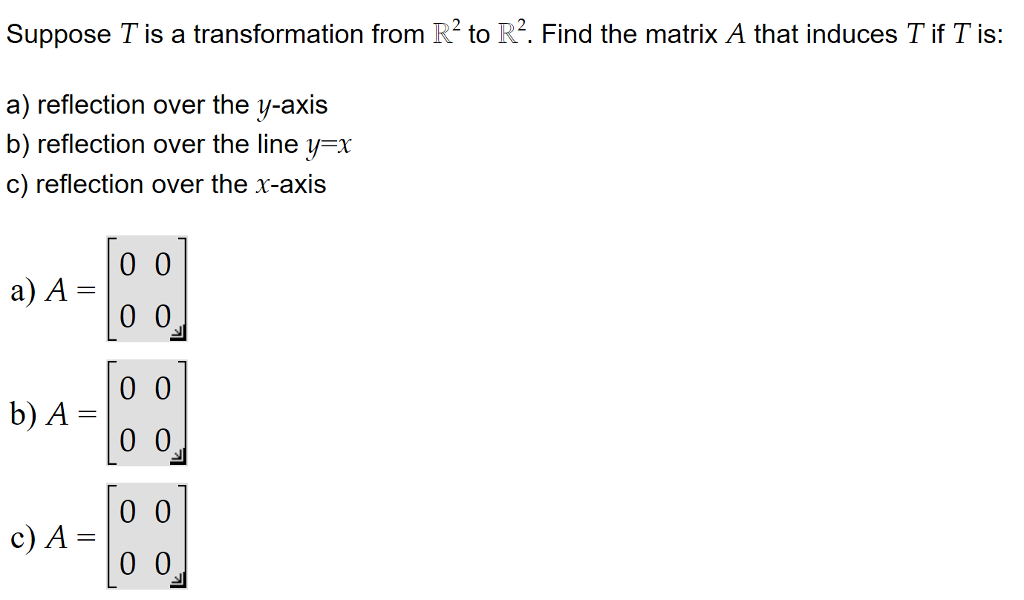
Reflection Definition In Geometry, a reflection is known as a flip A reflection is a mirror image of the shape An image will reflect through a line, known as the line of reflection A figure is said to be a reflection of the other figure, then every point in a figure is at equidistant from each corresponding point in another figureReflection through the axis Reflection through the line Reflection through the line Reflection through the origin Since for linear transformations, the standard matrix associated with compositions of geometric transformations is just the matrix product Problem find the Standard matrix for the linear Let $T\R^2 \to \R^2$ be a linear transformation of the $2$dimensional vector space $\R^2$ (the $x$$y$plane) to itself which is the reflection across a line $y=mx$ for some $m\in \R$ Then find the matrix representation of the linear transformation $T$ with respect to the standard basis $B=\{\mathbf{e}_1, \mathbf{e}_2\}$ of $\R^2$, where
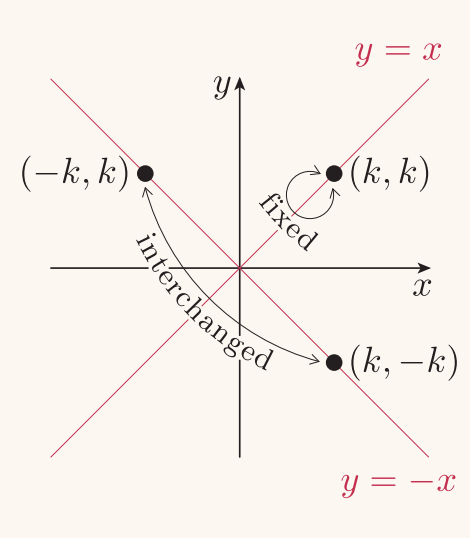
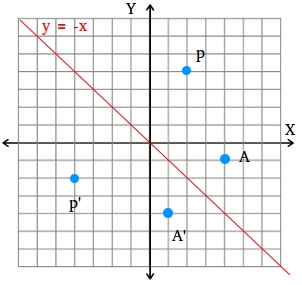
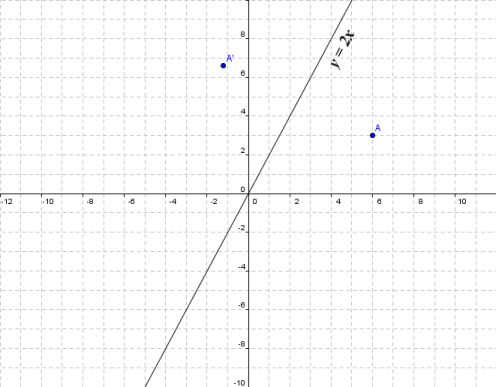
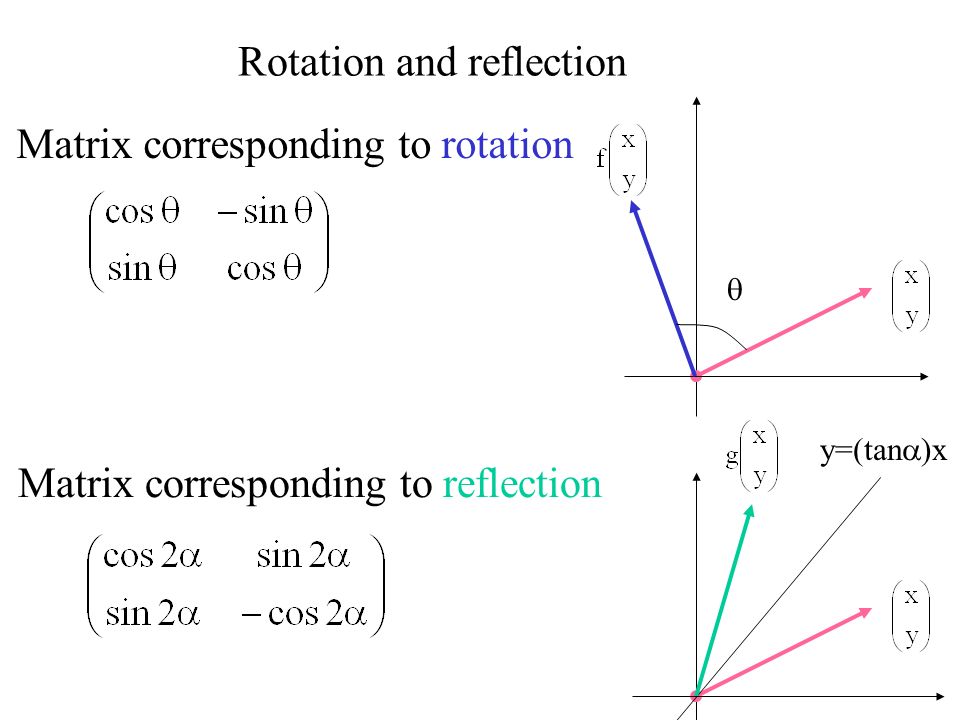
A good example is the reflection across the line y=x You can reflect the line y = 2x and it turns into the line 2y = x However, you find that the line y = x, after the reflection, is still y = x!X, y, z in the positive direction around thex axis for the angle α The axes x and x are collinear The rotational displacement is also described by a homogenous transformation matrix The first three rows of the transformationmatrix correspond to thex, y and z axes of the reference frame, while the first three columns refer to the x, y and Matrix formalism is used to model reflection from plane mirrors Start with the vector law of reflection kˆ kˆ 2(kˆ n)nˆ 2 = 1 − 1 • The hats indicate unit vectors k 1 = incident ray k 2 = reflected ray n = surface normal For a plane mirror with its normal vector n with (x,y,z) components (n x,n y,n z)
What does y=x mean in reflectionsのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 | ||
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
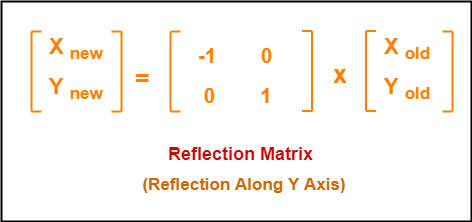 |  | |
 |  |  |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 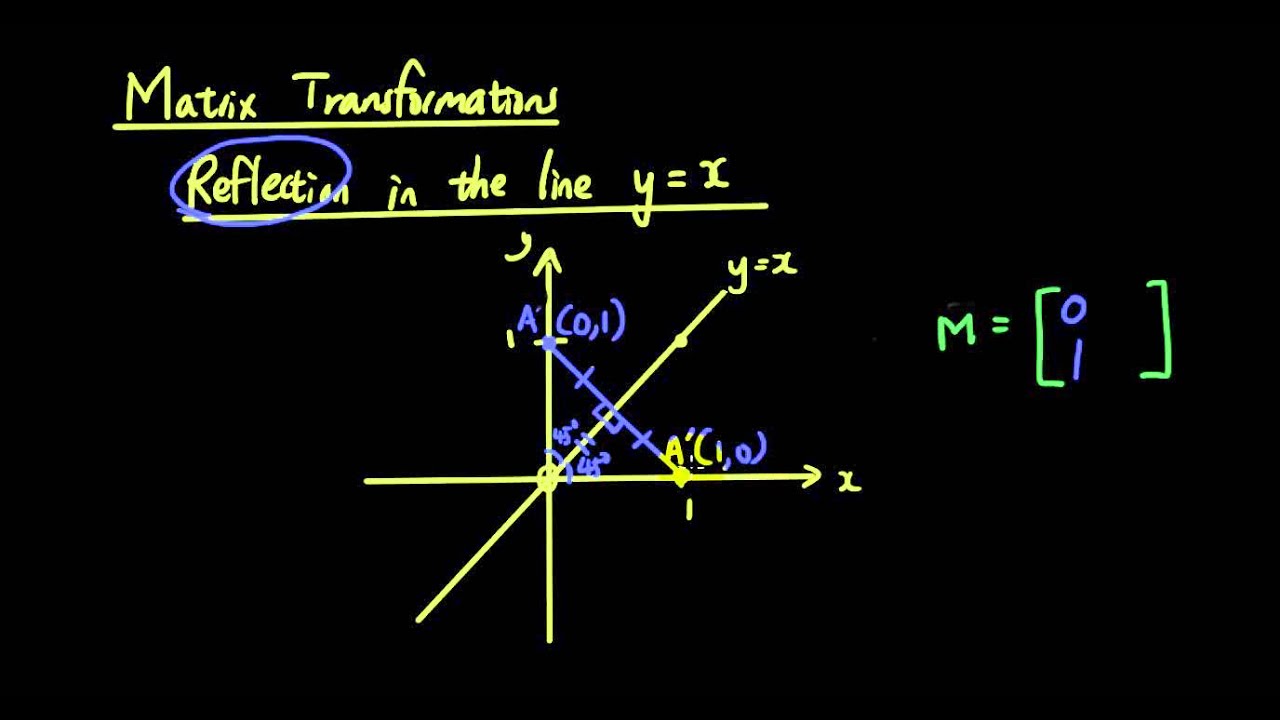 | 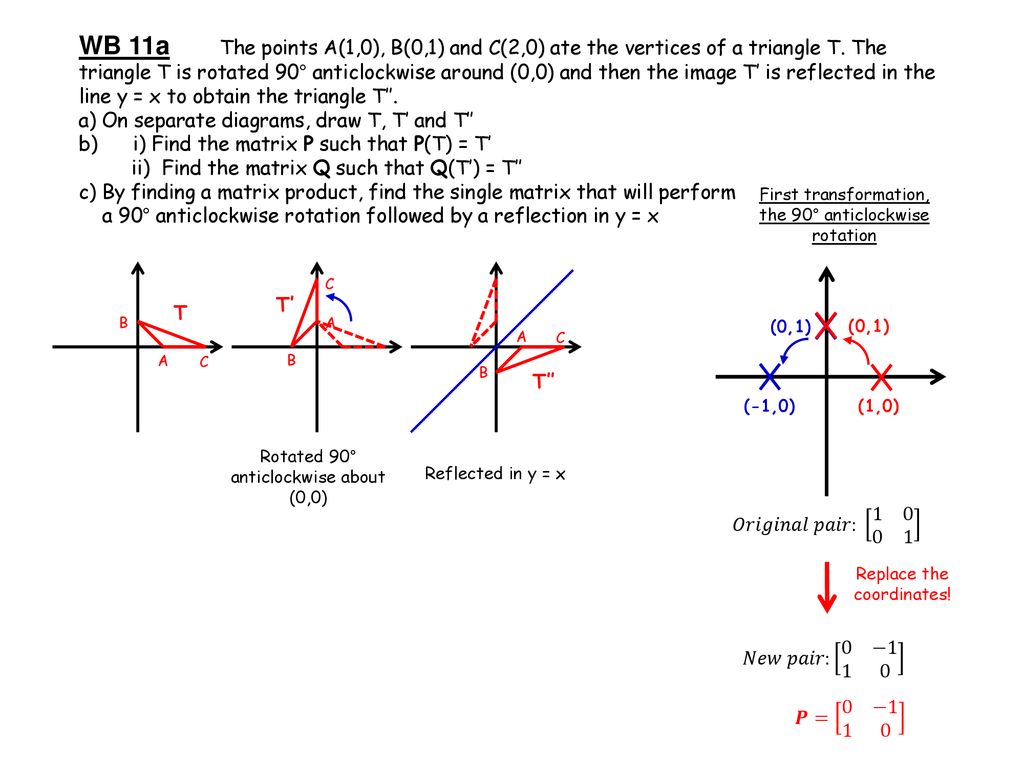 |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 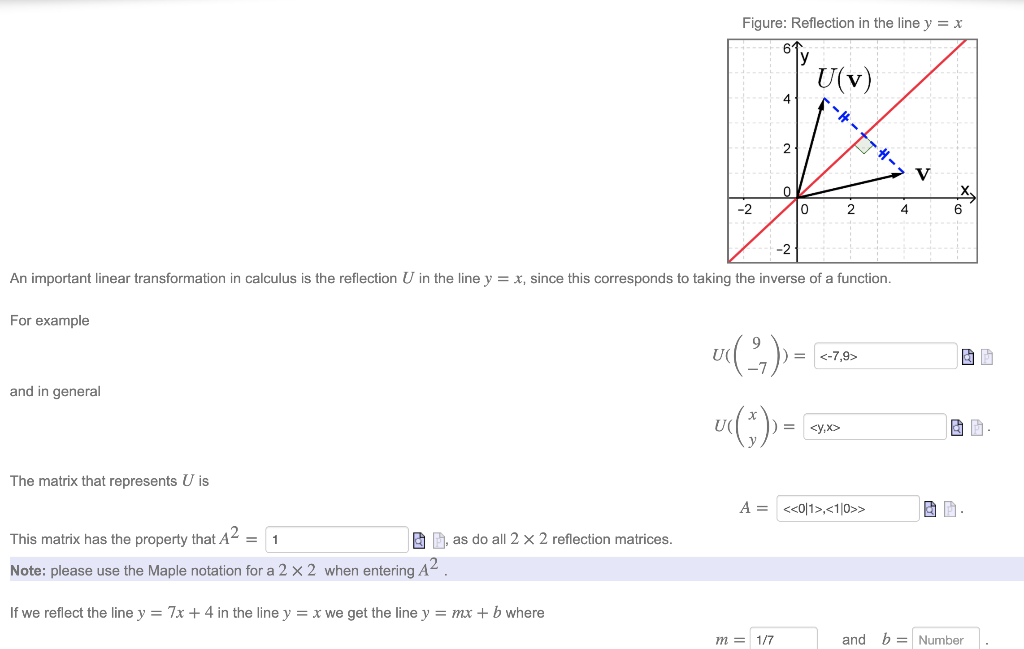 | 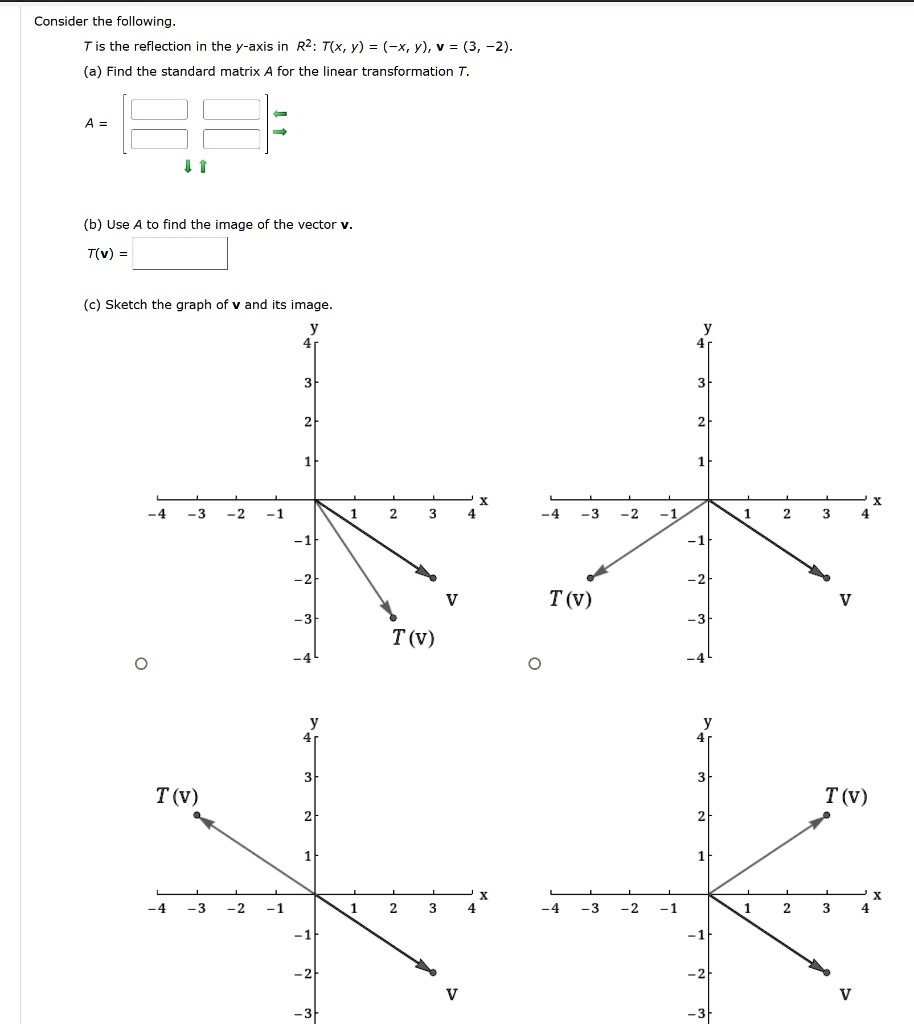 |
 | 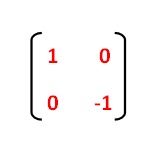 |  |
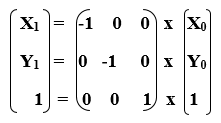 |  | 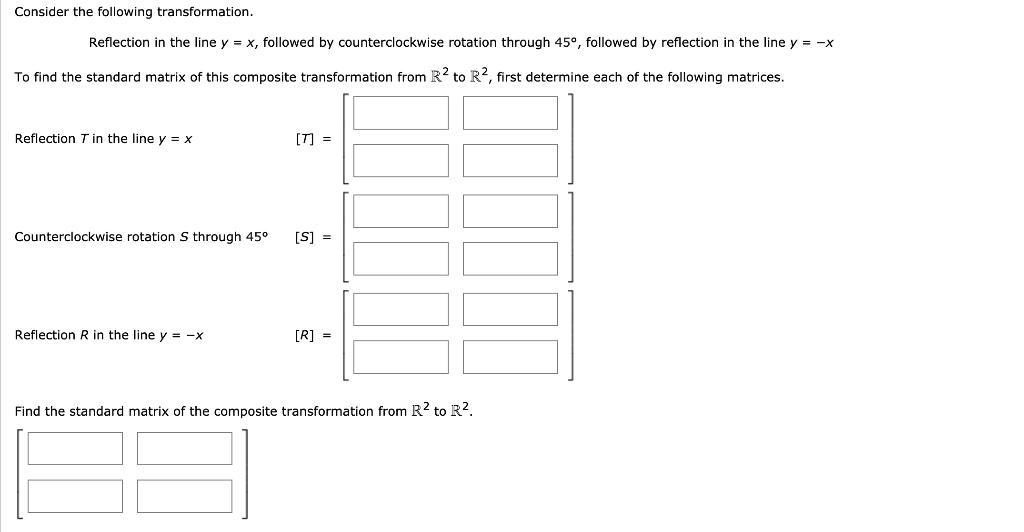 |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 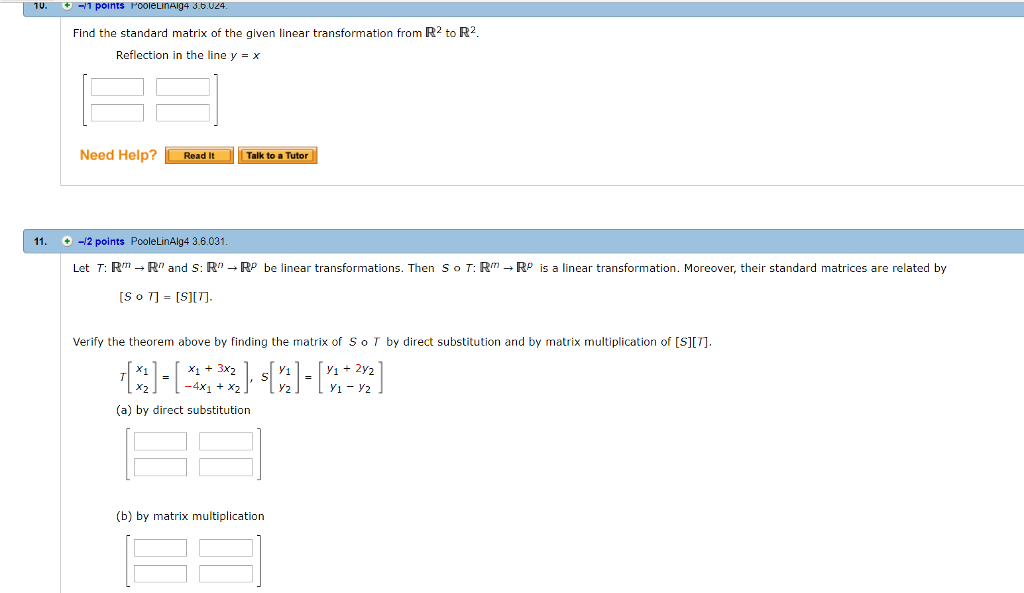 | 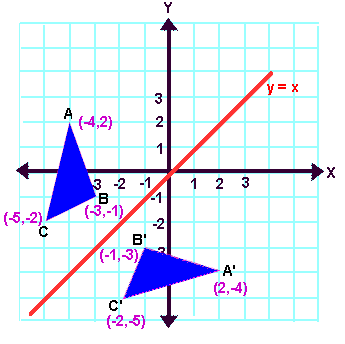 |
 | 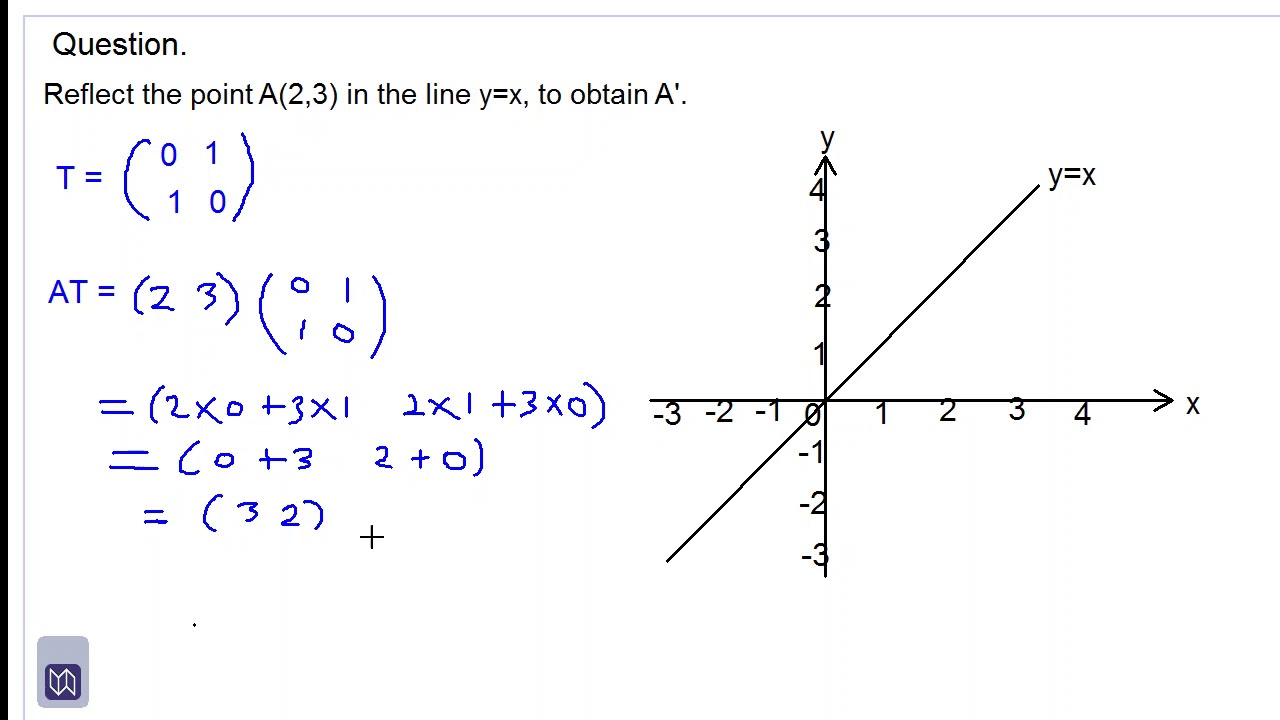 | 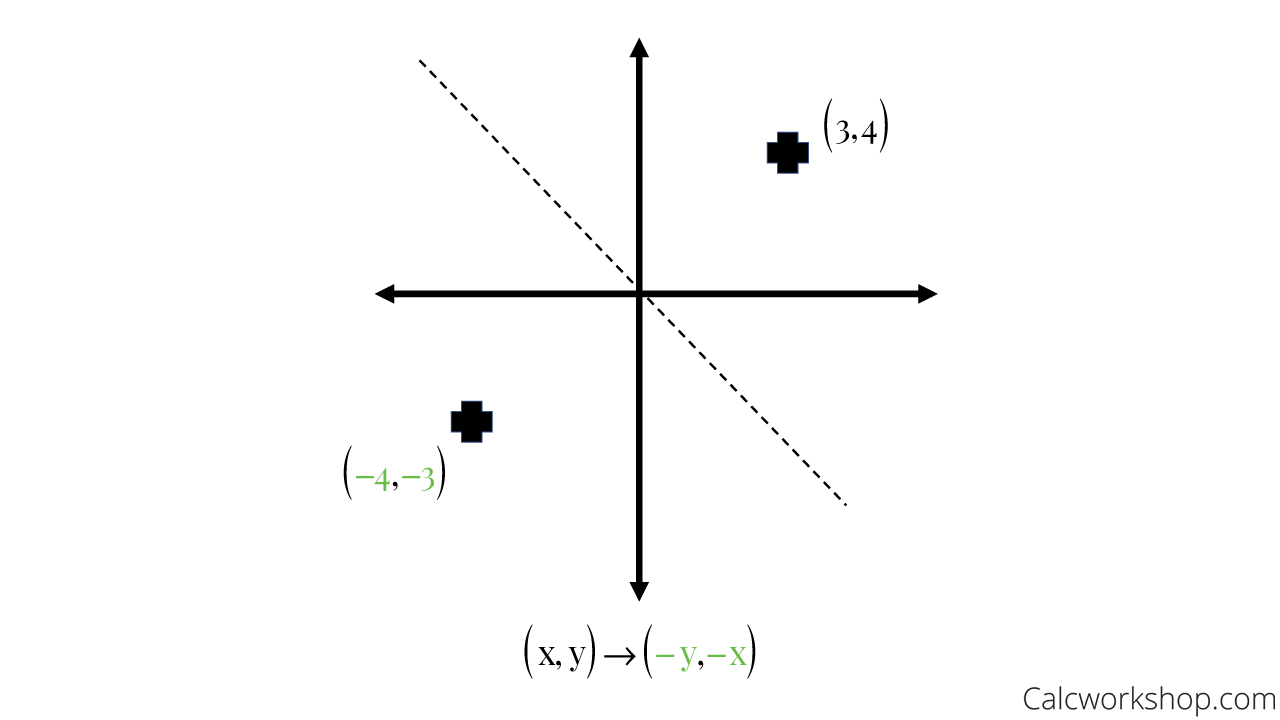 |
 | 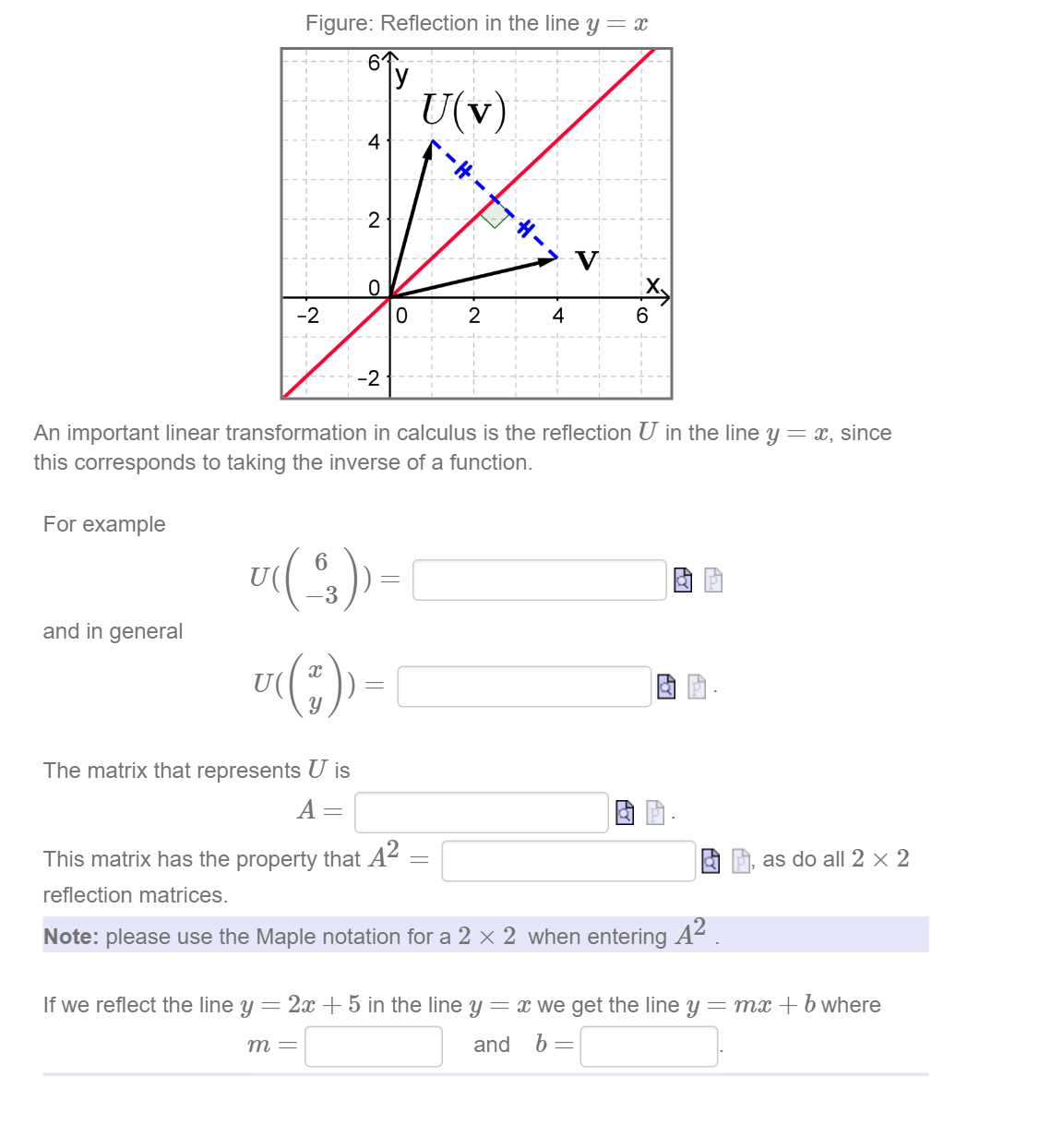 | |
「What does y=x mean in reflections」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
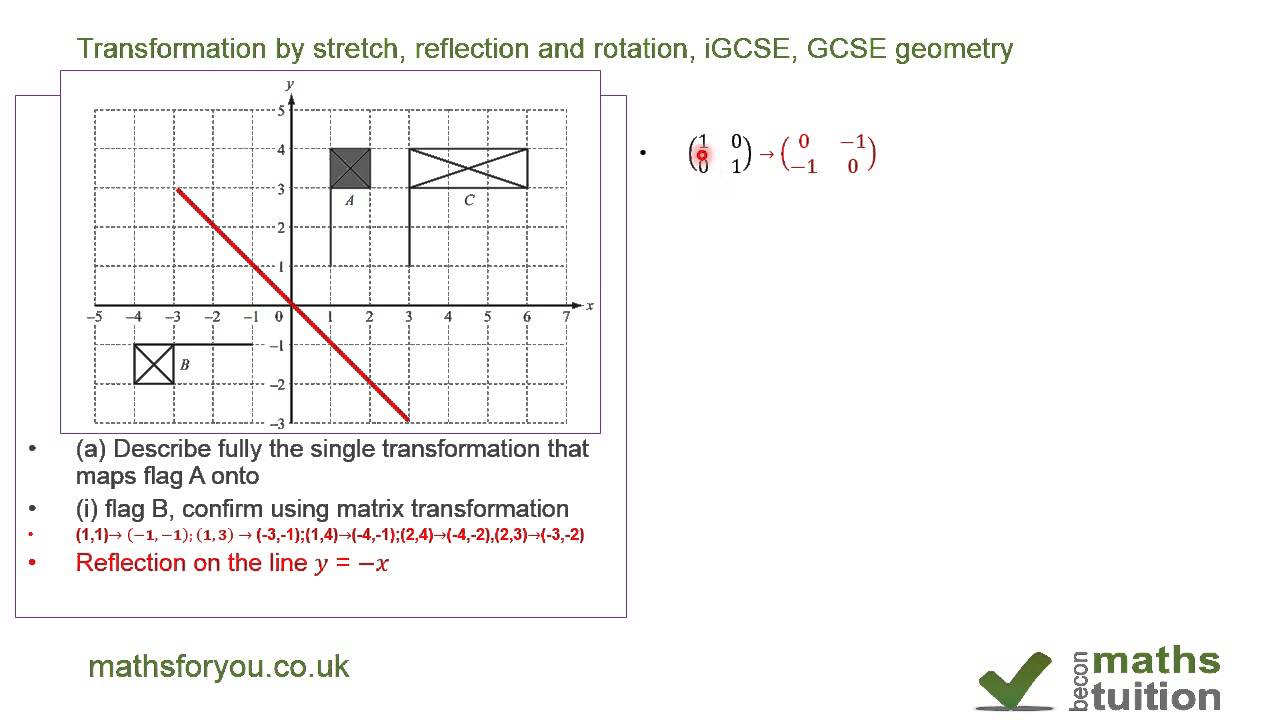
A Reflection at X axis B Reflection at Y axis C Reflection at origin D None of these ANSWER B The transformation matrix is used for_____ A Reflection at X axis B Reflection at Y axis C Reflection at origin D Reflection at line Y=X ANSWER C The transformation matrix is used for_____ A Reflection at origin B Reflection at X axisReplies 11 Views 14K F Find matrix The reflection should happen in the xzplane (with y=0) I've managed to render that into a FBO but currently there is some issue with the view or prespective matrix The reflection is either as seen from the wrong view position
Incoming Term: y=x reflection matrix, reflection over y=x matrix, how to do reflection y=x, what does y=x mean in reflections, what is a reflection matrix, what is reflection in the line y=x,



